Educational_Resources

Lecture 3: BST Add - Remove - Save

Created By: Yusuf Pisan

formatted to Github Markdown syntax by Ryan Peters

Be sure to check the other lectures out after you finish this one!

Previous lecture Next lecture

Table of Contents

  1. Overview
  2. TurtleProgram Grading Rubric
  3. UML Class Diagrams
  4. Huffman Coding
  5. Binary Search Tree (BST)
  6. Queue
  7. Heap
  8. Implementing Priority Queue as a Heap
  9. BST vs Heap in Implementing Priority Queue
  10. Heap Sort
  11. Ass-2: Binary Search Tree
  12. After Class

Overview

<meta name=”duration”content=”120”/>

TurtleProgram Grading Rubric

Automated tests Wednesday 10pm and Friday 10pm

Make sure getLength() is defined (number of strings in array)

Multiple criteria. 
-5 for partially correct, -10 for not working or missing - see comments

1. private dynamically allocated array of correct size (-20)
2. Constructors: Empty, 2 parameter and Copy Constructor
3. Destructor
4. <<
5. == and !=
6. =
7. + +=
8. * *=
9. getLength
10. setIndex / getIndex
11. memory leaks
12. efficiency and complexity
13. comments.txt - tested on CSS Linux Labs
14. Coding style + ass1.zip constructed properly

All files must be in subdirectory called ass1: ass1/turtleprogram.h, ass1/turtleprogram.cpp, ass1/comments.txt and ass1/comments.txt

Automated tests on Wednesday 10pm and Friday 10pm from “JollyFeedback”

UML Class Diagrams

UML for BinaryTree

UML ADT Queue

UML ADT Priority Queue

UML Class Diagrams (2)

From https://www.ibm.com/developerworks/rational/library/content/RationalEdge/sep04/bell/index.html

Savings Account inherits from Account

Account class is part of the Bank class

Account and ATM Transactions classes know each other

Huffman Coding

See example at http://courses.washington.edu/css343/zander/NotesProbs/huffmanexamples

Also some good BST information on http://courses.washington.edu/css343/zander/notes.html

Let’s do an example

d:4, r:6, s:6, h:6, i:7, n:7, a:8, t:9, o:8, e:13,

Letter Frequency from Wikipedia

Add - Binary Search Tree - Recursive Solution

add calls private function placeNode

placeNode(subTreePtr, newNodePtr)
  Search tree for newNodePtr
  if search terminates at the left subtree of the parentNode
    set leftChildPtr of parentNode to newNodePtr
  else
    set rightChildPtr of parentNode to newNodePtr

refining it (see textbook)

placeNode(subTreePtr, newNodePtr)
  if subTreePtr is nullptr
    return newNodePtr
  else if subTreePtr->getItem() >  newNodePtr->getItem()
    tempPtr = placeNode(subTreePtr->getLeftChildPtr(), newNodePtr)
    subTreePtr->setLeftChildPtr(tempPtr)
  else
    tempPtr = placeNode(subTreePtr->getRightChildPtr(), newNodePtr)
    subTreePtr->setRightChildPtr(tempPtr)
  return subTreePtr

Add - Binary Search Tree - Iterative Solution

If visiting all tree nodes, recursion is probably needed.

Add should not visit all tree nodes!

  if the rootPtr is nullptr
    set rootPtr, return
  else
    set curr to rootptr
    while not inserted
      if newNodePtr->item < curr->item
        if curr->left is nullptr
          add the new node to left
          set inserted to true
        else
          set curr to curr->left
      else
        // newNodePtr->item >= curr->item
        // same for right node

Remove - Binary Search Tree

Find the item and if found remove it and return true, else return false

There are 3 cases to consider when removing N

  1. N is a leaf - easy, set parent to nullptr

  2. N has one child - ok, promote child to N’s position

  3. N has two children - difficult

For Case 3, we need a different strategy.

  1. Pick another node M to remove.

  2. Copy the item in M to N’s location, therefore deleting the item at N.

  3. Remove the node M

How can we choose M so we preserve the BST properties?

All the items in N’s right subtree are greater than the item in N. Where is the smallest of these items? The leftmost branch of N’s rightChild! This item is called the inorder successor of N

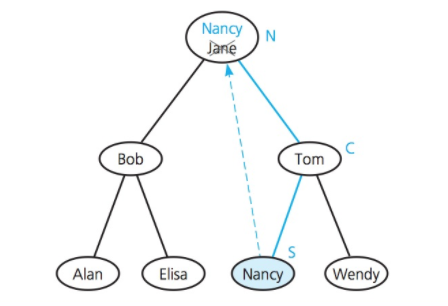
Removing inorder successor

Group Exercise: Removing Nodes

For each exercise below, start with the original tree above

  1. Remove 50, Remove 40

  2. Remove 20

  3. Remove 60

When to use Different Traversals

Inorder: sorted values

Preorder: clone tree, count nodes, prefix algebraic expression

Postorder: postfix algebraic notation, deleting tree

Saving BST to File or Array

Save the BST using inorder traversal, we get a sorted list of items, smallest to largest.

Reading it back, we want the middle item to be the root, so

If n is odd, read n/2 items as left subtree, read root, read n/2 items as right subtree

If n is even, one subtree needs to have one extra element.

Tree Sort

Add an array’s entries to BST.

Traverse BST in inorder, copy the values back to array

Additions: average O(log n), worst case O(n)
n additions: average O(n x log n), worst case O(n^2^)
traversal and copy: O(n) which is smaller than both average and worst case
tree sort: average case O(n x log n), worst case O(n^2^)

Re-Balancing a Binary Tree

What does it mean to be balanced?

AVL Trees - balanced binary search tree

https://en.wikipedia.org/wiki/Tree_rotation

We’ll get to them later!

Queue

FIFO - first in, first out (lunch queue, printer queue, …)

Implementation: Linked list

Implementation: Array based (keep track of front and back indexes)

More advanced version - circular array

Priority Queue

UML ADT Priority Queue

TODO Lists, Simulations

Implementation: Linked list

Heap

MaxHeap: Complete binary tree whose root is greater than its children

MinHeap: …

Not a binary search tree!

Heap - Array Based Implementation

Keep track of itemcount and maxItems

Heap - Add

Heap - Remove

Implementing Priority Queue as a Heap

Highest priority is at the root of MaxHeap

BST vs Heap in Implementing Priority Queue

If we know the maximum number of items in priority queue, heap is better

Heap is blanced, BST can become unbalanced degrading performance

If multiple items have the same priority, we can maintain a list at the node

When last item in the list deleted, node is deleted

Heap Sort

Ass-2: Binary Search Tree

Implement a BST

1. Add
2. Search
3. Inorder traverse
4. Height & Number of nodes
5. Rebalance
6. Add Multiple
10. Exit
>> 6
Enter multiple strings: g k d p i c a b
Added g
Setting right child of g to k
Added k
Setting left child of g to d
Added d
Setting right child of k to p
Added p
Setting left child of k to i
Added i
Setting left child of d to c
Added c
Setting left child of c to a
Added a
Setting right child of a to b
Added b
                p
            k
                i
        g
            d
                c
                        b
                    a
1. Add
...
3. Inorder traverse
...
10. Exit
>> 3
a b c d g i k p 

1. Add
2. Search
...
10. Exit
>> 2
Enter a string: i
Found i

1. Add
...
4. Height & Number of nodes
...
10. Exit
>> 4
Height: 5
Number of nodes: 8

After Class