Educational_Resources

Lecture 1 notes: Introduction & Trees

Created By: Yusuf Pisan

formatted to Github Markdown syntax by Ryan Peters

Be sure to check the other lectures out after you finish this one!

---

Table of Contents

1. Introduction and Trees
2. Overview
3. 342 Review
4. Reading Code (1)
5. Reading Code (2)
6. Reading Code (3)
7. Reading Code (4)
8. Reading Code (5)
9. Trees
10. Algebraic Expression
11. Binary Search Tree
12. After Class

---

Overview

http://courses.washington.edu/css343/pisan/

• Syllabus
  • Contact Info, Office Hours
  • Textbooks
  • Grading
  • Weekly Schedule
  • Resources

• About me

• Readings before class

---

342 Review

• Searching & Sorting
• Recursion
• Templates, STL
• Binary Search Tree
• Pointers, Linked Lists
• Stacks (LIFO), Queues (FIFO)
• Algorithm Analysis

Order them based on your level of comfort
https://pollev.com/pisan

---

Reading Code (1)

Somebody forgot to write comments!

int foo(int n)
{
   if (n  0)
      return 1;
   else
      return n * foo(n - 1);
}

What is its complexity? Why?

---

Reading Code (2)

int mystery(const int anArray[], int first, int last, int target)
{
   int index;
   if (first > last)
      index = -1;
   else
   {
      int mid = first + (last - first) / 2;
      if (target  anArray[mid])
         index = mid;
      else if (target < anArray[mid])
         index = mystery(anArray, first, mid - 1, target);
      else
         index = mystery(anArray, mid + 1, last, target);
   }
   return index;
}

What is its complexity? Why?

---

Reading Code (3)

template<class ItemType>
bool Grouch<ItemType>::mumble(const ItemType& newEntry)
{
   Node<ItemType>* nextNodePtr = new Node<ItemType>();
   nextNodePtr->setItem(newEntry);
   nextNodePtr->setNext(headPtr);

   headPtr = nextNodePtr;          
   itemCount++;
   
   return true;
}  // end add

What is its complexity? Why?

---

Reading Code (4)

SomeInterface, but what?

template<class ItemType>
class SomeInterface
{
public:
   virtual bool isEmpty() const = 0;
   virtual bool push(const ItemType& newEntry) = 0;
   virtual bool pop() = 0;
   virtual ItemType peek() const = 0;
   virtual ~SomeInterface() {  }
};

---

Reading Code (5)

template<class ItemType>
void someSort(ItemType theArray[], int n)
{
   bool sorted = false;
   int pass = 1;
   while (!sorted && (pass < n))
   {
      sorted = true;
      for (int index = 0; index < n - pass; index++)
      {
         int nextIndex = index + 1;
         if (theArray[index] > theArray[nextIndex])
         {
            std::swap(theArray[index], theArray[nextIndex]);
            sorted = false; // Signal exchange
         } // end if
      }  // end for
      
      pass++;
   }  // end while
}  // end someSort

What is its complexity? Why?

---

Trees

• Single root, hierarchical - more than one immediate successor
• nodes, edges
• child, parent, sibling, ancestor, descendant
• subtree
• general, n-ary, binary tree
• height (root at level 1, empty tree has height 0)

---

Algebraic Expression

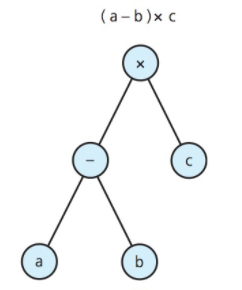
Representing (a - b) x c

• Traversal
  • preorder - root, left, right
  • inorder - left, root, right
  • postorder - left, right, root

Let’s try different traversals.

Group Exercise: ((a + b) * (c + d)) / (e * f) - g

---

Binary Search Tree

search(BST, target)
  if (BST is empy)
    item not found
  else if target  data in BST
    item found
  else if target < data
    search(left subtree, target)
  else
    search(right subtree, target)

What is the worst case complexity for a badly constructed tree?

Create a balanced BST for A, B, C, D, E, F

---

After Class

Explore the Resources on course pages

Read/Review Binary Search Trees

Read Math (Rosen) 11.1-3 (available under Resources)

Logon to #slack https://css-uwb.slack.com/ join #343 and give an example of a programming error that you tend to make

Assignment 1: TurtleProgram

• Abstract Data Type (ADT) defines behavior.
• Data Structure is a concrete implementation of ADT
• Ask questions - but you have to debug your own code

Start programming